Το λοιπόν, άλλαξα πάλι το www.dimjt.gr, βασικά το έκανα μάλλον ομορφότερο, όμως (όπως και συμβαίνει συνήθως στο ίντερνετ) πιο ‘βαρύ’ και για να δω τι μπορεί να κάνει το νέο μας skin, αφού έχω συμπληρώσει παντού εικόνες (ναι, και από ΑΙ!), παίζω πάλι με το WordPress και ρίχνω ένα μαθηματικό αρθράκι που αφορά τα ποσοστά και το πως έχουν μπει για τα καλά στη ζωή μας!

Έχετε όρεξη για μαθημα;

Έχετε δεν έχετε, θα το κάνουμε!

Καταρχήν, πως υπολογίζουμε ένα ποσοστό αύξησης με εύκολο και γρήγορο τρόπο;

Ας πούμε ότι η τιμή της φέτας έχει πάει στα 12 ευρώ το κιλό, ενώ πέρσι ήταν στα 10 ευρώ το κιλό (τυχαίο – χαχαχα – παράδειγμα).

Ένας απλός τρόπος υπολογισμού του πόσο έχει ανέβει είναι να διαιρέσουμε το μεγαλύτερο με το μικρότερο ποσό, δηλαδή:

12/10 = 1,2

Τώρα, τι ν’ τούτο;

Τούτο είναι το ποσοστό της αύξησης και εξηγώ αμέσως:

Ένα ποσοστό εκφράζεται επί τοις 100, όμως το 100% είναι πάντα το 1! (ελπίζω να μη σας χάνω…100% σημαίνει φουλ, ολόκληρο, δηλαδή 100/100, δηλαδή 1).

Γυρνάω στο παράδειγμα.

Αφού το 100% είναι το 1, αγνοούμε τον άσο μπροστά από το 1,2 και έχουμε 0,2 ή (το ίδιο πράγμα) 0,20 σαν αποτέλεσμα, ή αλλιώς (βάζουμε και το ποσοστό τώρα):

20% αύξηση στη φέτα!

Πάμε επαλήθευση:

Στα 10 ευρώ που ήταν πέρσι βάζω επιπλέον 20% δηλαδή το 1/5 (20/100 = 1/5), δηλαδή τον αριθμό 2 (αφού είπαμε το 1/5 και 10/5 κάνει 2) και τι έχουμε;

10 + 2 = 12 ευρώ η φετούλααααααα

Έλα δεν είναι δύσκολο, μην παραπονιέστε.

Για όσους/ες παραπονιούνται παρόλα αυτά:

Ας πούμε πάρτε το σαν κανόνα:

Διαιρούμε το μεγαλύτερο με το μικρότερο και από ότι προκύψει αγνοούμε τον άσο μπροστά και παίρνουμε το νούμερο μετά το κόμμα.

ΑΥΤΟ είναι το ποσοστό αύξησης.

ΠΡΟΣΟΧΗ!!!

ΔΕΝ ισχύει ο παραπάνω κανόνας σε περίπτωση που κάτι έχει μείωση (εδώ μπορείτε να γελάσετε άφοβα!).

Για παράδειγμα, ας πούμε ότι πέφτει ένα προϊόν από τα 10 ευρώ στα 8 ευρώ.

Για να δούμε τι ισχύει, με βάση τον κανόνα:

10/8 = 1,25

Αγνοούμε το 1, άρα έπεσε κατά 25% το προϊόν(;;;;).

Όντως;

Όχι, διότι το 25% είναι στην ουσία 25/100 ή αλλιώς 1/4 και το 1/4 του 10 είναι το 2,5 άρα θα έπρεπε η τιμή του να πάει στα 7,5 ευρώ.

Στην πραγματικότητα έπεσε κατά 20% πάλι (το 1/5 του 10).

Άρα:

Δεν χρησιμοποιούμε τον κανόνα εύρεσης ποσοστού σε περίπτωση μείωσης, αλλά μόνο σε περίπτωση αύξησης!

Το γιατί ακριβώς είναι μαθηματικό ζήτημα και δεν μας ενδιαφέρει.

Αλλά, από την άλλη, στην καθημερινότητά μας πλέον, υπάρχει κάτι που έχει πέσει (σε τιμή) ρε παιδιά εκεί έξω και δεν το ξέρω;

Εδώ το εισιτήριο (ενιαίο) του ΟΑΣΘ και του ΜΕΤΡΟ Θεσσαλονίκης θα πάει στο 1,1€ από 0,9€ (να πω ότι δεν τα έλεγα; τα έλεγα!) και μπορεί να μην του φαίνεται αλλά είναι πάνω από 20% αύξηση:

1,1/0,9 = 1,2222222222222222222

Άρα 22,22% αύξηση.

Βρε δεν μας χέζετε που έχετε αυξήσει το κόστος ζωής στο θεό και δεν μπορούμε να τα βγάλουμε πέρα ούτε με αίτηση;

Το ξέρετε, το ξέρω και το ξέρουν:

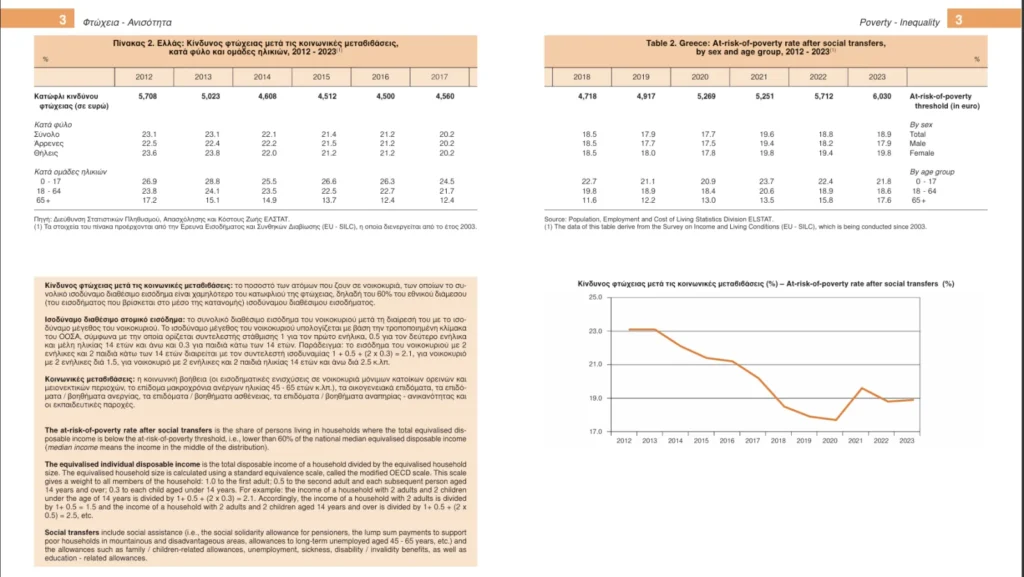
Ο κίνδυνος φτώχειας μετά μετά τις κοινωνικές μεταβιβάσεις, δηλαδή το ποσοστό των ατόμων που ζουν σε νοικοκυριά, των οποίων το συνολικό ισοδύναμο διαθέσιμο εισόδημα είναι χαμηλότερο του κατωφλιού της φτώχειας.

Η παραπάνω εικόνα (για να σας δώσω να καταλάβετε, το ποσοστό που βλέπετε παίζει από 23% μέχρι το 18% και μάλιστα τελευταία ανεβαίνει πάνω από το 19%) είναι ένα μικρό δείγμα από την πλήρη αναφορά της Ελληνικής Στατιστικής Αρχής που μπορείτε να βρείτε ολόκληρη παρακάτω (σε μορφή PDF):

SYNTHIKES_DIAVIOSIS_new (statistics.gr)

ΟΚ, λένε οι δείκτες ότι διάφορα ‘κακά πράγματα μειώνονται’ ή διάφορα ‘καλά πράγματα αυξάνονται’ αλλά, πέρα από το παραπάνω που αυξάνεται (miracolo, miracolo!), λένε, ας πούμε οι δείκτες ότι έχει μειωθεί η ανεργία στο 10% περίπου, αλλά, ρε μλκες, αυτό σημαίνει κοντά στα 500.000 άτομα να πούμε, βγαίνετε και πανηγυρίζετε ότι έχετε μειώσει την ανεργία από την εποχή της κρίσης;

Και λέω από την εποχή της κρίσης του 2010 γιατί πολλά πράγματα μετριούνται από τότε, αλλά ρε σεις πέρασαν και 14 χρόνια και για όλα φταίνε τα μνημόνια ακόμα;

Έλεος.

Το θέμα είναι ότι η ακρίβεια μας έχει τσακίσει, το πιτόγυρο κοντεύει στα 5 ευρώ και δεν κουνιέται ούτε ρουθούνι, τα τρώμε όλα αμάσητα (pun intended!).

Για να γυρίσω, όμως, στο καυτό θέμα (πραγματικά!!) των ποσοστών, μετά από πολλά χρόνια έμαθα και κάτι ΥΠΕΡ-χρήσιμο που αφορά το Φ.Π.Α. (ο οποίος είναι ένα ποσοστό, σωστά;).

Καλά, το ότι όλα τα αγαθά φορολογούνται το ξέρουμε και το περιμένουμε, το ΦΠΑ δεν περιμέναμε να φτάσει στο 24% αλλά τέλος πάντων, έτσι είναι τα πράγματα.

Τώρα, αυτό είναι ήδη ποσοστό, οπότε ξεχάστε ότι έχουμε πει μέχρι τώρα για τα ποσοστά, διότι δεν ισχύουν, αφού δεν ψάχνουμε ποσοστό αλλά το έχουμε έτοιμο και αυτό είναι το γνωστό: 24%.

ΧΡΥΣΟΣ ΚΑΝΩΝ:

• Αν θέλουμε να βρούμε την τιμή χωρίς ΦΠΑ ενός προϊόντος που περιλαμβάνει τον ΦΠΑ, τότε διαιρούμε με τον αριθμό: 1,24
• Αν θέλουμε να βρούμε την τελική τιμή ενός προϊόντος το οποίο δεν έχει αρχικά ΦΠΑ, τότε πολλαπλασιάζουμε με τον ίδιο αριθμό: 1,24.

Άρα, αν σας πουν ότι χαρίζουν το ΦΠΑ, κάντε ένα τσεκ και μόνοι σας, για να δείτε τι εννοούν.

Διότι, για παράδειγμα, σας συμφέρει να σας μειώσουν ένα ποσό κατά 24% (όπως παρακάτω):

62€ – 24% = 47,12€ (λάθος τρόπος αποφορολόγησης)

Ενώ, δεν σας συμφέρει (στην περίπτωση αυτή) να σας ‘κόψουν το ΦΠΑ’, διότι:

62€ / 1,24 = 50€ (σωστός τρόπος αποφορολόγησης)

Στο πενηντάρικο, δηλαδή, μπαίνει ‘καπέλο’ ΦΠΑ 12 ολόκληρα ευρώ, διότι, αντίστροφα:

50€ x 1,24 = 62€

Αρκετά μαθηματικά για σήμερα, μοιράσαμε πάλι τη γνώση αλλά και την από-γνωσή μας απλόχερα και ελπίζουμε να σταματήσουμε να τα μετράμε όλα κάποια στιγμή στο άμεσο μέλλον και όχι…στην άλλη τη ζωή!

Υ.Γ.: Τα χάλια μας σε αριθμούς, για τους hardcore αριθμολάγνους εκεί έξω: Κεντρική Σελίδα ΕΛΣΤΑΤ – ELSTAT (statistics.gr)

Υ.Γ.2: Αν ο ΦΠΑ μειωθεί πότε…τότε απλά αλλάζετε το 1,24 στο νέο ποσοστό, π.χ. 1,23 αν πάει στο 23% ή 1,22 αν πάει στο 22% κ.ο.κ. Που δεν θα κατέβει ποτέ, αλλά τέλος πάντων…υπομονή και…φέεεεεεεετα (αχ, φέτα, μονάκριβή μου φέτα)!